Research

My research interests include

• Statistical inference for networks: latent space models, community detection, dynamic and multilayer networks, Bayesian inference.

• Statistical learning and data science: classification, regression, dimension reduction, clustering, visualization, random forests and trees, deep learning.

• Bayesian methodology: Monte Carlo methods, variational inference, Bayesian nonparametrics, scalable computation.

Statistical Network Analysis

Modeling the dynamics of complex social systems is an essential component of many applied problems. To understand the formation and dissolution of international alliances, predict regional conflicts such as the Arab Spring and the emergence of ISIS, and forecast the trajectory of infectious disease spread throughout a community, we need models of each complex system’s dynamics. As such, my research develops statistical models that infer vital characteristics within the observed dynamics of complex systems. My work in this area focuses in addressing estimation and inference problems by exploiting low-dimensional representations using a combination of latent space models, hidden Markov models, linear dynamical systems, and Bayesian inference. I have developed new statistical models for analyzing dynamic and multilayer networks, including methodology for community detection, prediction, forecasting, and the estimation of missing data. I have also introduced widely applicable variational inference procedures that allow for estimation in large networks.

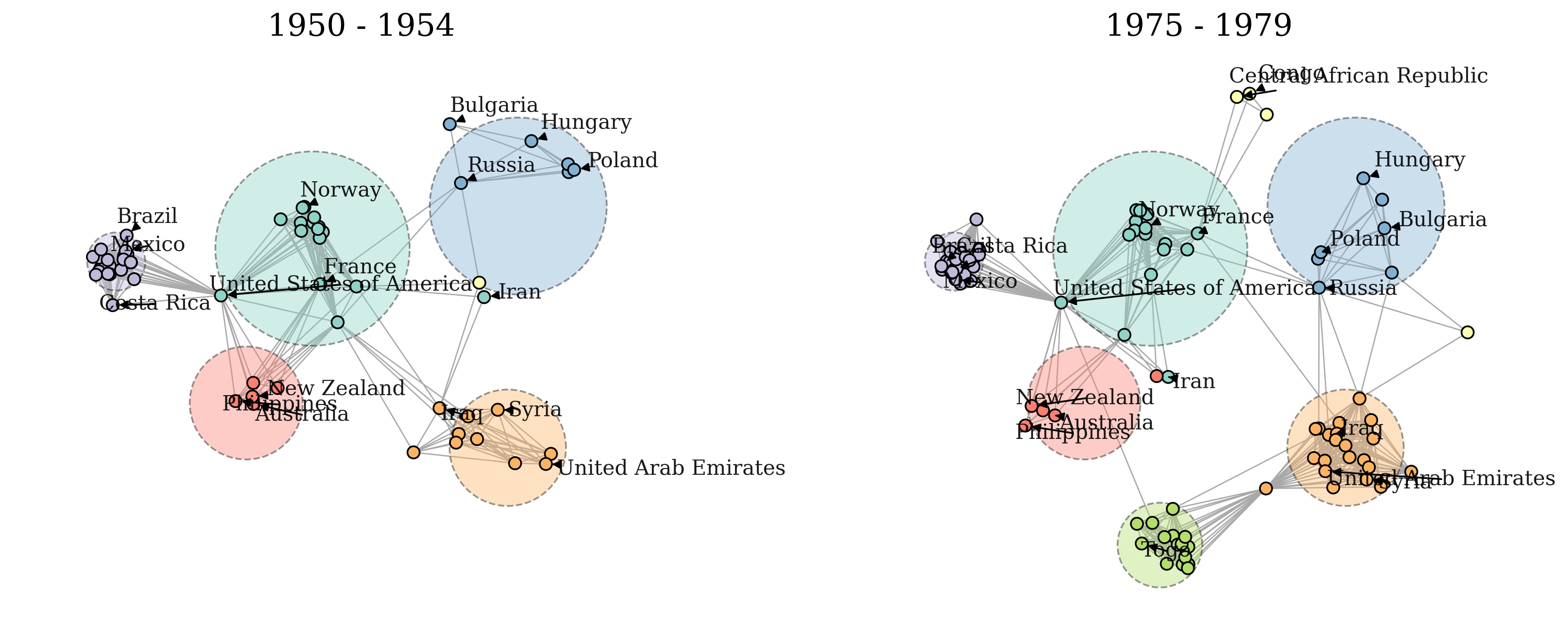
References

• Loyal, J.D., Chen, Y. (2022). A Bayesian nonparametric latent space approach to modeling evolving communities in dynamic networks. Accepted at Bayesian Analysis. [article] [code]

• Loyal, J.D., Chen, Y. (2022). An eigenmodel for dynamic multilayer networks. Invited revision. [preprint] [code]

• Loyal, J.D., Chen, Y. (2020). Statistical network analysis: A review with applications to the coronavirus 2019 pandemic. Accepted at International Statistical Review. [article]

Statistical Learning and Data Science

Modern problems in statistical learning and data science are increasingly concerned with interpreting the results of powerful black-box estimators. For example, fields such as personalized medicine, policy-making, and bioinformatics currently require flexible estimators that can infer variable importance and reduce the dimension of the problem. My past work has exploited local low-dimensional structure in the data to provide interpretable solutions without losing flexibility. Specifically, I developed new techniques to infer local variable importance by using a combination of random forests and sufficient dimension reduction. Such local variable importance measures have applications in personalized medicine where the ability to tailor medical treatment to patients based on their unique genetic makeup can drastically decrease patient mortality.

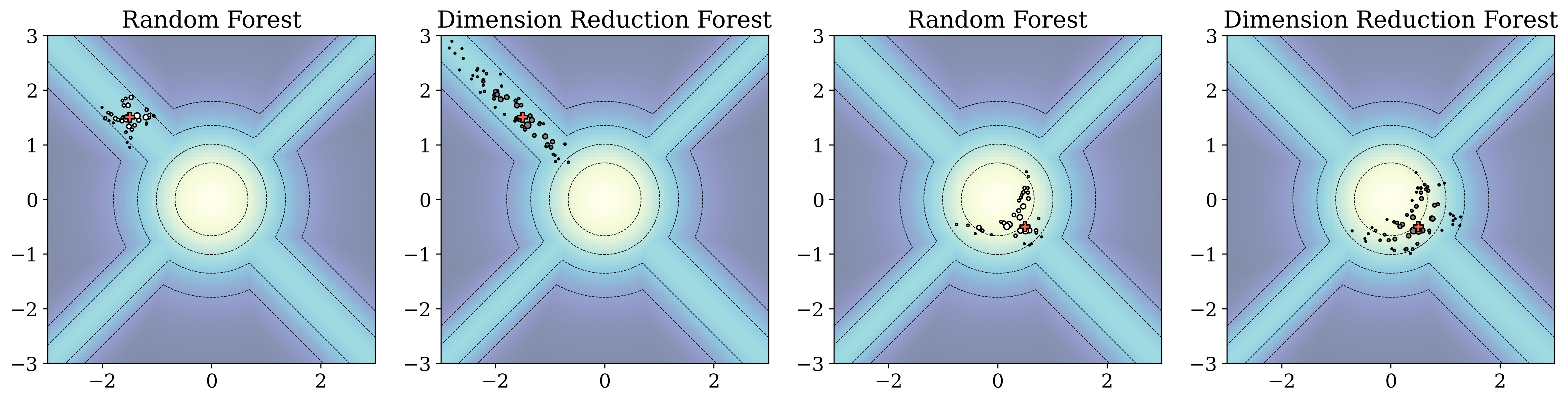
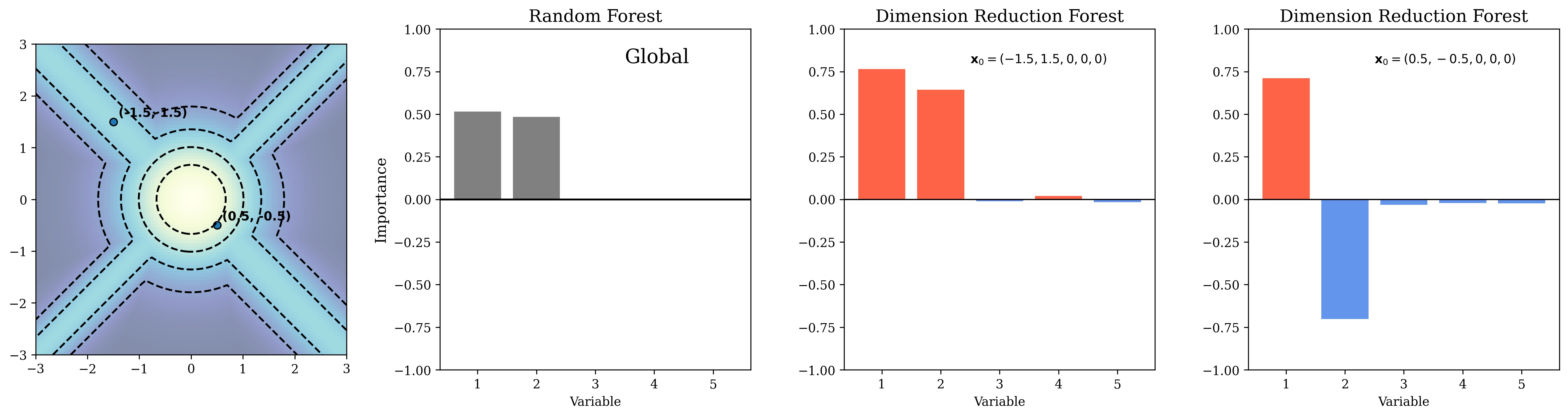
References:

• Loyal, J.D., Zhu, R., Cui, Y., and Zhang, X. (2022). Dimension reduction forests: Local variable importance using structured random forests. Accepted at Journal of Computational and Graphical Statistics. [article] [code]